Evaluation of parameter uncertainties in nonlinear regression using Microsoft Excel Spreadsheet

Wei Hu; Jing Xie; Henry Wai Chau; Bing Cheng Si

doi:10.1186/s40068-015-0031-4

Research article

Open Access

Evaluation of parameter uncertainties in nonlinear regression using Microsoft Excel Spreadsheet

Wei Hu¹,
Jing Xie¹,
Henry Wai Chau² and
Bing Cheng Si¹Email author

Environmental Systems Research20154:4

https://doi.org/10.1186/s40068-015-0031-4

Received: 22 January 2015

Accepted: 11 March 2015

Published: 24 March 2015

Abstract

Background

Nonlinear relationships are common in the environmental discipline. Spreadsheet packages such as Microsoft Excel come with an add-on for nonlinear regression, but parameter uncertainty estimates are not yet available. The purpose of this paper is to use Monte Carlo and bootstrap methods to estimate nonlinear parameter uncertainties with a Microsoft Excel spreadsheet. As an example, uncertainties of two parameters (α and n) for a soil water retention curve are estimated.

Results

The fitted parameters generally do not follow a normal distribution. Except for the upper limit of α using the bootstrap method, the lower and upper limits of α and n obtained by these two methods are slightly greater than those obtained using the SigmaPlot software which linearlizes the nonlinear model.

Conclusions

Since the linearization method is based on the assumption of normal distribution of parameter values, the Monte Carlo and bootstrap methods may be preferred to the linearization method.

Keywords

BootstrapMonte CarloSoil water retentionParameter uncertaintyExcel

Background

Nonlinear relationships are common in natural and environmental sciences (Wraith and Or 1998; Luo et al. 2003; Cwiertny and Roberts 2005). As a result, there are many software packages (such as SAS and MathCAD) that implement nonlinear parameter estimation. However, spreadsheet techniques are easier to learn than other specialized mathematical programs for nonlinear parameter estimation, because no programming skills are needed in spreadsheets to develop their own parameter estimation routines (Wraith and Or 1998). In addition, spreadsheets have the merits of wide accessibility and powerful computation in terms of fitting nonlinear models. For these reasons, spreadsheets such as Microsoft Excel are widely suggested to make nonlinear parameter estimation (Harris 1998; Smith et al. 1998; Wraith and Or 1998; Brown 2001; Berger 2007).

Parameter uncertainty refers to lack of knowledge regarding the exact true value of a quantity (Tong et al. 2012). Different observations are usually obtained when experiments are repeated, resulting in different values of parameters. It is usually expressed as an interval of parameter values at a certain confidence level, say, 95%. It is also expressed as the standard error of the mean by assuming normal distribution of parameter values. Parameter uncertainty can be used to judge the degree of reliability of the parameter estimates, which is important to making decisions for environmental management. For these reasons, estimation of parameter uncertainties is significant for nonlinear parameter estimates. However, relatively less work has focused on the nonlinear parameter uncertainty estimates using spreadsheet packages.

Parameter uncertainty can be obtained exactly by assuming normal distribution of a parameter in linear regression, but not in nonlinear regression. Nonlinear regression programs usually give the parameter uncertainty by calculating the standard error of the mean, and assuming linear relationship between variables in the vicinity of the estimated parameter values and normal distribution of parameter values. Furthermore, this method usually involves evaluating a Hessian matrix (a square matrix of second-order partial derivatives of a scalar-valued function to describe the local curvature of a function of many variables) or an inequality, which makes it more complicated and time demanding (Brown 2001). More general methods such as Monte Carlo and bootstrap simulation can be used to estimate the parameter uncertainties. Both methods have their own advantages: while the Monte Carlo method is based on a theoretical probability distribution of a variable, the bootstrap method has no assumption on the probability distribution of a variable and thus has no limits on sampling size. Among numerous related applications are testing fire ignition selectivity of different landscape characteristics using the Monte Carlo simulation (Conedera et al. 2011) and estimating uncertainty of greenhouse gas emissions using the bootstrap simulation (Tong et al. 2012). However, parameter uncertainties estimation in spreadsheets using the Monte Carlo and bootstrap methods has been rarely discussed.

Both nonlinear parameter values and their associated uncertainties are important for decision making and thus should be implemented in spreadsheet program like Excel. Microsoft Excel spreadsheets have other advantages including their general facility for data input and management, ease in implementing calculations, and often advanced graphics and reporting capabilities (Wraith and Or 1998). These advantages are likely to make the use of spreadsheets to quantify parameter uncertainties more desirable.

The objective of this paper is to apply the Monte Carlo and bootstrap simulations to obtain parameter uncertainties with a Microsoft Excel spreadsheet. In addition, the influences of number of simulation on uncertainty estimates are also discussed. For this, we use as an example, a common soil physical property - soil water retention curve, which has been widely used in soil, hydrological, and environmental communities.

Results and discussion

Nonlinear regression parameters estimation

Here are the steps to estimate parameters α and n in Excel using nonlinear regression.

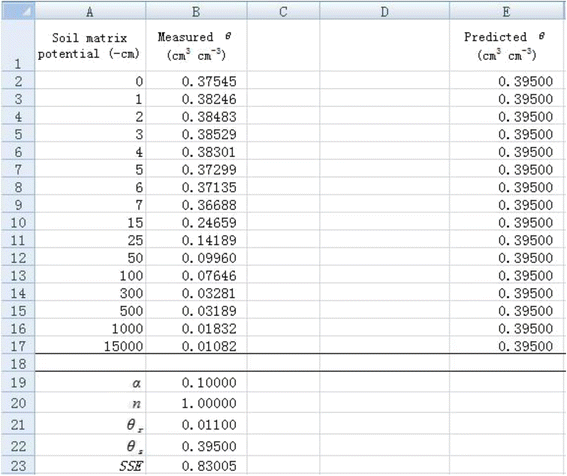
1. List the applied suction pressure as the independent variable in column A and measured soil water content (θ) as the dependent variable in column B (Figure 1).

Figure 1
**Data input and initial value set for** α **and** n **in a spreadsheet.**

2. Temporarily set the value of α as 0.1 and n as 1 in cells B19 and B20, respectively (Figure 1). It is important to set an appropriate initial value because an obviously unreasonable initial value will lead to an unanticipated value. Please refer to related document for initial value estimation (e.g., Delboy 1994). List the measured θ _r and θ _s in cells B21 and B22, respectively. Then the predicted θ value can be calculated with the van Genuchten soil water retention curve model (Eq. 5) using suction pressure and all parameter values. For example, the predicted θ in cell E2 ($ {\widehat{\theta}}_{E2} $) is calculated by the following formula:

$$ {\widehat{\theta}}_{E2}=\$B\$21+\left(\$B\$22-\$B\$21\right)\ast \left(1+\left(\$B\$19\ast \$A2\right)\hat{\mkern6mu} \$B\$20\right)\hat{\mkern6mu} \left(-1+1/\$B\$20\right) $$

(1)

As Figure 1 shows, all the predicted θ values are 0.395 given the initial values.

3. Calculate the sum of squared residuals (SSE) using Excel function SUMXMY2 in cell B23 by entering “SUMXMY2(B2 : B17, E2 : E17)”. We obtain 0.83005 for SSE for the given initial parameter values (Figure 1).

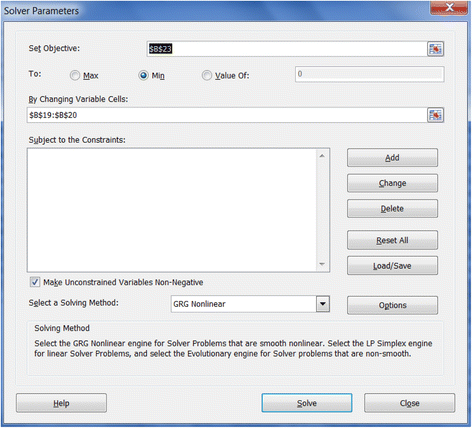
4. The model obtains the maximum likelihood when the SSE is minimized, which is the principle of least-square fitting method. The Solver tool in Excel can be used to minimize the SSE values. The Solver tool can be found under the Data menu in Excel. If not found there, it has to be added from File menu through the path File- > Options- > Add-Ins- > Solver Add-in. As Figure 2 shows, the “Set Objective” box is the value to be optimized, which is the SSE value in cell B23. Click “Min” to minimize the objective SSE by changing the values of α and n as shown in the “By Changing Variable Cells”.

Figure 2
**Solver working screen in Excel 2010.**

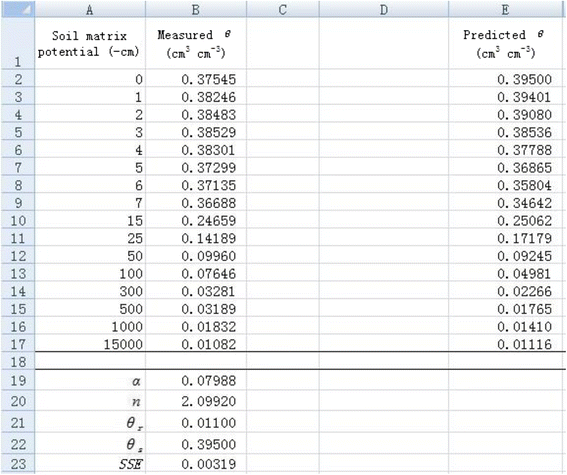
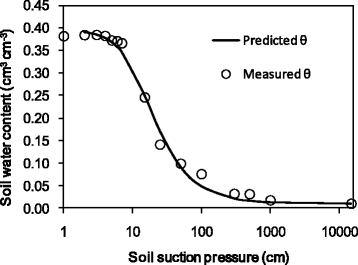
5. The Solver will then find the minimum SSE (in cell B23) and corresponding α (in cell B19) and n (in cell B20) values (Figure 3). The measured θ values are in agreement with the predicted θ values (Figure 4), indicating a good nonlinear curve fitting.

Figure 3
**A spreadsheet for estimating nonlinear regression coefficients** α **and** n .

Figure 4
**Measured and predicted soil water content versus soil suction pressure.**

Using Monte Carlo method to estimate parameter uncertainty

Stepwise application of the Monte Carlo method in estimating parameter uncertainties with 200 simulations is demonstrated below:

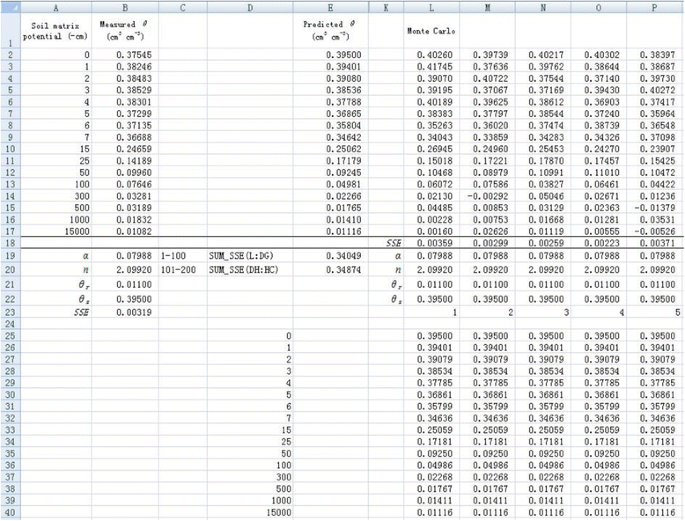
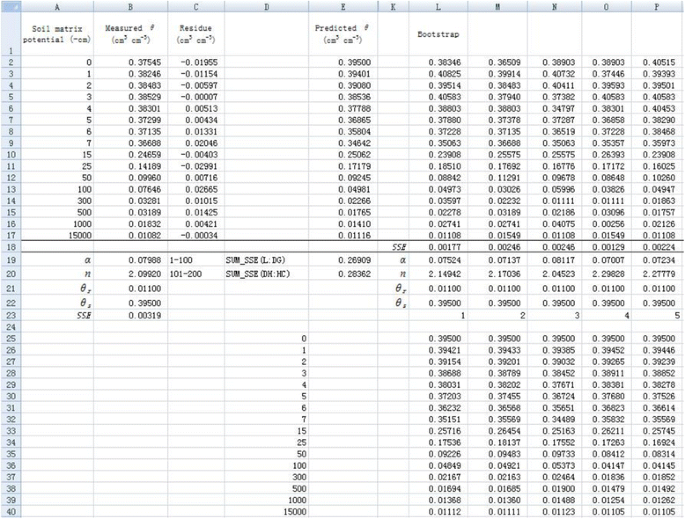
1. Resample θ using the Monte Carlo method in different columns. Take cell L2 for example, the simulated θ (θ _L2) is calculated by the following formula:

$$ {\theta}_{L2}=\$\mathrm{E}2+\mathrm{NORM}.\mathrm{I}\mathrm{N}\mathrm{V}\left(\mathrm{RAND}\left(\right),0,\mathrm{SQRT}\left(SSE/df\right)\right) $$

(2)

where $E2 refers to the corresponding predicted θ. SSE is the value calculated above, which is the value in cell B23 in Figure 5. The degree of freedom (df) equals 14. The θ values in the other rows in column L are simulated in a similar way. The simulated values for a new dependent variable θ are demonstrated in cells L2-L17 (Figure 5). The same Monte Carlo simulations are performed from column M to column HC. Therefore, a total of 200 sets of simulated θ are obtained (Figure 5).

Figure 5
**Resampling dependent variable** θ **using Monte Carlo method and initial values set (only the first 5 simulations are shown).**

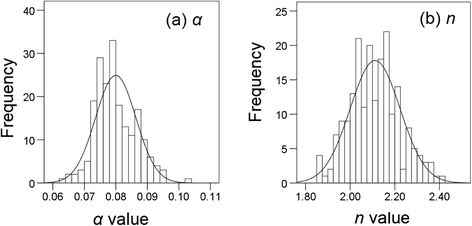
2. Use the same procedure as introduced before to conduct nonlinear regression for each new data set of θ. Note that the new data set of θ will change during optimization, which will result in errors in fitting. Therefore, we copy the simulated θ data to a new sheet by right-clicking “Paste Special” and selecting “Values” in the dialogue of “Paste Special”. For better display, predicted θ array, all the parameter values, and corresponding SSE value are presented in the same column for each simulation (Figure 5). Optimization of parameters α and n is made independently for each simulation using the Solver tool. The initial values are set as the fitted values obtained before for all simulations to reduce the time required during the optimization. Therefore, initial values of 0.07988 and 2.09920 are set for α and n, respectively (Figure 5). Because the maximum number of variables Solver can solve is 200, we can minimize the SSE values for 100 simulations at one time by minimizing the sum of SSE values of 100 simulations. For example, the parameters α and n for the first 100 simulations can be optimized by minimizing cell E19 by entering “=SUM(L18:DG18)” (Figure 5). Similarly, the parameters for the second 100 simulations can be optimized in cell E20 by entering “=SUM(DH18:HC18)”. Therefore, we obtain 200 values for both parameters (α and n) as shown in cells from L19 to HC20 (Figure 6). The frequency distribution of α and n are shown in Figure 7. Visually, both of them follow a normal distribution. However, the Shapiro-Wilk test shows that the parameter α does not conform to a normal distribution, whereas parameter n does. This indicates that the fitted parameters may not necessarily be normally distributed even if the dependent variable is normally distributed, due to the nonlinear relations between them.

Figure 6
**Nonlinear regression fitting for resampled** θ **using Monte Carlo method (only the first 5 simulations are shown).**

Figure 7
**Frequency distribution of (a)** α **and (b)** n **obtained using Monte Carlo method with 200 simulations.** The heights of bars indicate the number of parameter values in the equally spaced bins. The curve is the theoretical normal distribution.

3. Calculate the 95% confidence interval of α or n values with 200 simulations. We copy all the fitted α or n values, then paste them to a new sheet by right-clicking “Paste Special” and selecting “Transpose” in the dialogue of “Paste Special” to list all the fitted α or n values in one column. Select the transposed data, and rank them in an ascending order using Sort tool in Data tab. Find the value of α and n corresponding to the 2.5 percentile and 97.5 percentile, which are the lower limit and upper limit, respectively, at a 95% confidence. The 95% confidence interval are (0.0680, 0.0939) and (1.9185, 2.3689) for α and n, respectively (Table 1). The difference between upper limit and lower limit is 0.0259 and 0.4504 for α and n, respectively.

Table 1

Comparison of parameter uncertainties calculated by different methods

Parameter		Monte Carlo	Bootstrap	Linearization
α	Lower limit	0.0680	0.0680	0.0670
	Upper limit	0.0939	0.0925	0.0928
	Upper limit-Lower limit	0.0259	0.0245	0.0258
n	Lower limit	1.9185	1.9172	1.8758
	Upper limit	2.3689	2.3356	2.3218
	Upper limit-Lower limit	0.4504	0.4184	0.4460

Using bootstrap method to estimate parameter uncertainty

Stepwise application of the bootstrap method in estimating parameter uncertainties with 200 simulations is demonstrated as follows:

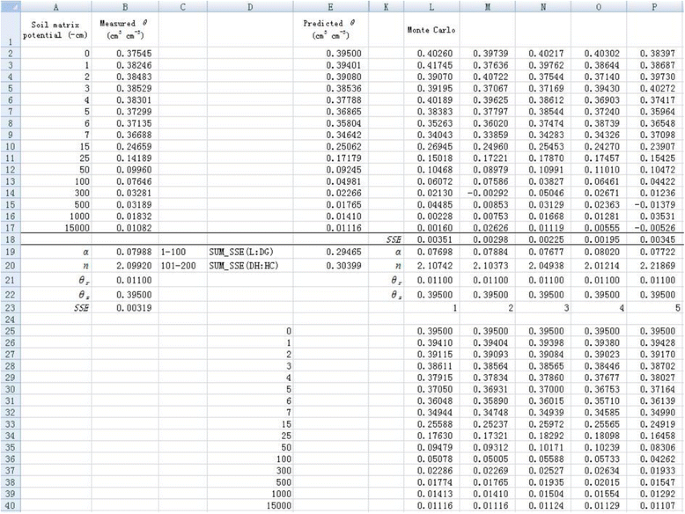
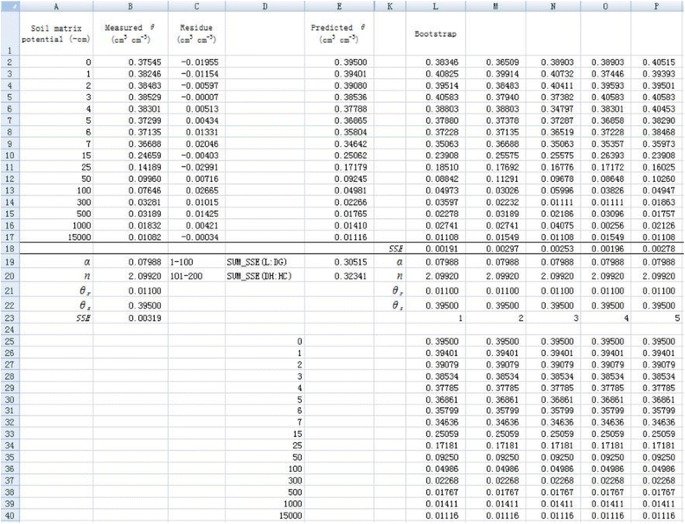
1. Resample θ using the bootstrap method in different columns (Figure 8). Take cell L2 for example, the simulated θ (θ _L2) can be calculated by the following formula:

Figure 8
**Resampling dependent variable** θ **using bootstrap method and initial values set (only the first 5 simulations are shown).**

$$ {\theta}_{L2}=\$\mathrm{E}2+\mathrm{INDEX}\left(\$\mathrm{C}:\$\mathrm{C},\mathrm{I}\mathrm{N}\mathrm{T}\left(\mathrm{RAND}\left(\right)*16+2\right)\right) $$

(3)

where the function INDEX is used to randomly select a residue value from row 2 to row 17 in column C (the residual is calculated by subtracting predicted θ from the original θ). The θ values at other rows in column L and in other columns (column M to column HC) are simulated in a similar way. Here, 2 in the right hand side of Eq. (3) means that data start at second row.

2. Similar to the Monte Carlo method, parameters α and n for all simulations are fitted by minimizing the sum of every 100 SSE values using the Solver tool (Figures 8 and 9). Therefore, we can also obtain 200 values for both parameters (α and n) as shown in cells from L19 to HC20 (Figure 9). The frequency distribution of α and n are shown in Figure 10. They also visually follow a normal distribution. However, the Shapiro-Wilk test shows that the parameter α does not conform to normal distribution, whereas parameter n does.

Figure 9
**Nonlinear regression fitting for resampled** θ **using bootstrap method (only the first 5 simulations are shown).**

Figure 10
**Frequency distribution of (a)** α **and (b)** n **obtained using bootstrap method with 200 simulations.** The heights of bars indicate the number of parameter values in the equally spaced bins. The curve is the theoretical normal distribution.

3. Similar to the Monte Carlo method, the 95% confidence intervals for these two parameters are calculated. They are (0.0680, 0.0925) and (1.9172, 2.3356), for α and n respectively (Table 1). The corresponding difference between upper limit and lower limit is 0.0245 and 0.4183 for α and n, respectively.

Influences of number of simulation on parameter uncertainty analysis

Datasets of fitted values with different numbers of simulations are obtained using a similar method as demonstrated before (data not shown). According to Shapiro-Wilk test, both parameters do not follow a normal distribution with different numbers of simulations except for a few cases that the number of simulations ≤400. This may indicate that the assumption of normality in the linearization method does not hold true.

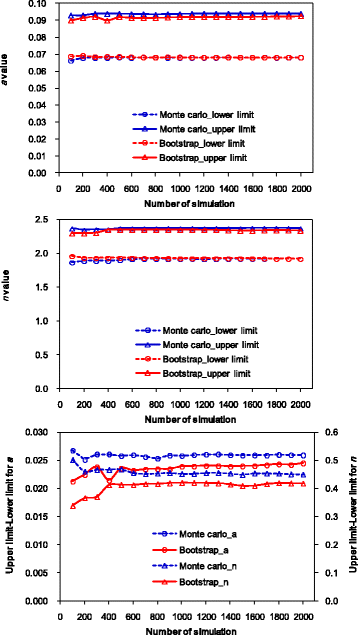
The lower limit, upper limit, and their difference change slightly with the number of simulations. However, they are almost constant beyond a certain number of simulations (Figure 11). Here, we determine the number of simulations required for both methods according to the change in difference between the upper limit and lower limit. If the relative difference (RD%) of the difference between the upper limit and lower limit under a certain number of simulation is less than 5% compared with that under 2000 simulations, the number of simulations tested is taken to be the required number of simulations. The RD% can be calculated as

$$ \mathrm{R}\mathrm{D}\%=\left|\frac{{\mathrm{V}}_m-{\mathrm{V}}_{2000}}{{\mathrm{V}}_{2000}}\right|*100\% $$

(4)

where V_m and V₂₀₀₀ are the differences between the upper limit and lower limit under m simulations and 2000 simulations, respectively.

Figure 11
**Influences of number of simulation on the lower limit, upper limit, and difference of upper limit and lower limit.**

For the Monte Carlo method, the RD% is less than 5% for α and n when the numbers of simulation are ≥100 and 200, respectively. For the bootstrap method, the RD% is less than 5% for α and n when the numbers of simulation are ≥500 and 400, respectively. Therefore, simulation number of 200 and 500 are needed to produce reliable data at the 95% confidence interval of parameters for the Monte Carlo and bootstrap methods, respectively. In this sense, the Monte Carlo method may be better than the bootstrap method. However, the optimal number of simulation may also differ with specific situations. For example, Efron and Tibshirani (1993) stated that a minimum of approximately 1000 bootstrap re-samples was sufficient to obtain accurate confidence interval estimates. In order to obtain reliable confidence interval estimates, we suggest increasing the simulation times by 100 at each step, and the final results can be obtained when the values stabilize within consecutive steps.

Comparison with parameter uncertainty approximated by linear model

The values α and n are estimated to be 0.0799 and 2.0988, respectively, by SigmaPlot 10.0 (Figure 12), which are exactly the same as the estimates made by nonlinear regression in Excel. Based on the linear model, the associated standard errors are estimated to be 0.0066 and 0.1138, respectively (Figure 12). Then the 95% confidence intervals of α and n are (0.0670, 0.0928) and (1.8758, 2.3218), respectively. As Table 1 shows, the difference between upper limit and lower limit by the Monte Carlo and bootstrap methods are comparable, although the Monte Carlo method produces a slightly greater uncertainty than the bootstrap method. The slight difference is due to the differences in re-sampling residues. While the Monte Carlo simulation generates residues based on a theoretical normal distribution, the bootstrap method randomly takes the residues with replacement and no assumption is made about the underlying distributions. They are also comparable to those approximated by the linear model obtained from the SigmaPlot software. However, by comparing the results of these three methods, the lower limit and upper limit of α and n obtained by the Monte Carlo and bootstrap methods are slightly greater than those obtained based on a linear assumption except for upper limit of α by the bootstrap method. Because the linearization method is based on the assumption of normal distribution of parameters and linearity at the vicinity of the estimated parameter value, and it is more complicated in terms of calculation, the Monte Carlo and bootstrap methods may be preferred to the linearization method to calculate the parameter uncertainties in spreadsheets. Furthermore, the Monte Carlo method may be preferred to the bootstrap method considering the less number of simulations required for the Monte Carlo method. However, if the number of measurements is too small to determine the probability distribution for Monte Carlo method, the bootstrap method may be superior.

Figure 12
**Estimates of parameters (** α **and** n **) and associated standard errors using SigmaPlot 10.0.**

Conclusions

This paper shows step-by-step how to use a Microsoft Excel spreadsheet to fit nonlinear parameters and to estimate their uncertainties using the Monte Carlo and bootstrap methods. Both Monte Carlo and bootstrap methods can be applied in Excel spreadsheets to resample a large number of measurements for dependent variable from which different values of parameters can be obtained. Our results clearly show that the Monte Carlo and bootstrap methods can be used to estimate the parameter uncertainties using spreadsheet methods. The main limitation is that one execution of standard Microsoft Excel Solver has a limit of 200 simultaneous optimizations. This limit can be overcome by multiple independent executions of Solver. Due to the wide accessibility of Microsoft Excel software and ease of use for these two methods, employing the Monte Carlo and bootstrap methods in spreadsheets is strongly recommended to estimate nonlinear regression parameter uncertainties.

In this paper, we demonstrated the methodology with the van Genuchten water retention curve. The method can be applied to any mathematical functions or models that can be evaluated by Excel. Therefore, the methodology presented in this paper has wide applicability. Further, with little modification, the Monte Carlo method or bootstrap method can be used in Microsoft Excel to estimate the uncertainty of hydrologic or environmental predictions with single or multiple input parameters under different degrees of uncertainty.

Methods

Soil water retention curve

Soil water content is a function of soil matric potential ψ under equilibrium conditions, and this relationship θ(ψ) can be described by different types of water retention curves. The soil water retention curve is a basic soil property and is critical for predicting water related environmental processes (Fredlund et al. 1994). Among various soil water retention curve models, the van Genuchten (1980) model is the most widely used one (Han et al. 2010). It is highly nonlinear and can be expressed as:

$$ \theta \left(\uppsi \right)={\theta}_r+\left({\theta}_s-{\theta}_r\right){\left(1+{\left(\alpha \left|\uppsi \right|\right)}^n\right)}^{-1+\frac{1}{n}} $$

(5)

where θ(ψ) is the soil water content [cm³ cm⁻³] at soil water potential ψ (−cm of water), θ _r is the residual water content [cm³ cm⁻³], θ _s is the saturated water content [cm³ cm⁻³], α is related to the inverse of the air entry suction [cm⁻¹], and n is a measure of the pore-size distribution (dimensionless). We measured θ(ψ) at 16 soil water potentials for a sandy soil using Tempe pressure cells (at soil matrix potentials ranging from 0 to −500 cm) and pressure plates (at soil water potentials of −1000 and −15000 cm). θ _s is measured using oven drying method after saturation, and θ _r is estimated as water content of soil approaching air-dry conditions (Wang et al. 2002). θ _s and θ _r are 0.395 and 0.011, respectively. Note that the soil water content (0.375) at zero matrix potential is lower than θ _s due to the soil water movement under gravity. This paper will focus on the estimation of parameters α and n and their associated 95% confidence intervals.

Parameter uncertainty estimation by linearization of nonlinear model

We express the van Genuchten model (Eq. 5) as:

$$ {\theta}_i=f\left(\beta, {\uppsi}_i\right)+{\varepsilon}_i $$

(6)

where θ _i is the i th observation for the dependent variable θ(ψ) (i = 1, 2, …16), ψ_i is the i th observation for the predictor |ψ|. β is a vector of parameters which includes parameters α and n. ε _i is a random error, which is assumed to be independent of the errors of other observations and normally distributed with a mean of zero and variance of σ ².

The sum of squared residuals (SSE) for nonlinear regression can be written as:

$$ SSE\left(\beta \right)={\displaystyle \sum }{\left({\theta}_i-f\left(\beta, {\uppsi}_i\right)\right)}^2 $$

(7)

The model has the maximum likelihood when the SSE is minimized. Namely, when the partial derivative

$$ \frac{\partial SSE\left(\beta \right)}{\partial \beta }=-2{\displaystyle \sum}\left({\theta}_i-f\left(\beta, {\uppsi}_i\right)\right)\frac{\partial f\left(\beta, {\uppsi}_i\right)}{\partial \beta } $$

(8)

is zero, parameters β are optimized. Once the optimum values of β are obtained, the parameter uncertainties can be estimated by linearizing the nonlinear model function at the optimum point using the first-order Taylor series expansion method (Fox and Weisberg 2010).

Let

$$ {\boldsymbol{F}}_{\boldsymbol{ij}}=\frac{\partial f\left(\widehat{\beta},{\uppsi}_i\right)}{\partial {\beta}_j} $$

(9)

where $ \widehat{\beta} $ is the optimized value, j refers to the jth of parameters (j = 1, 2, and β ₁ = α, β ₂ = n).

Assume matrix F = [F _ij]. In our case,

$$ \boldsymbol{F}=\left[\begin{array}{cc}\hfill \frac{\partial f\left(\widehat{\beta},{\psi}_1\right)}{\partial \alpha}\hfill & \hfill \frac{\partial f\left(\widehat{\beta},{\psi}_1\right)}{\partial n}\hfill \\ {}\hfill \frac{\partial f\left(\widehat{\beta},{\psi}_2\right)}{\partial \alpha}\hfill & \hfill \frac{\partial f\left(\widehat{\beta},{\psi}_2\right)}{\partial n}\hfill \\ {}\hfill \vdots \hfill & \hfill \vdots \hfill \\ {}\hfill \frac{\partial f\left(\widehat{\beta},{\psi}_{16}\right)}{\partial \alpha}\hfill & \hfill \frac{\partial f\left(\widehat{\beta},{\psi}_{16}\right)}{\partial n}\hfill \end{array}\right] $$

(10)

where $ \frac{\partial f\left(\widehat{\beta},{\uppsi}_i\right)}{\partial \alpha } $ and $ \frac{\partial f\left(\widehat{\beta},{\uppsi}_i\right)}{\partial n} $ can be calculated by the following formulae:

$$ \frac{\partial f\left(\widehat{\beta},{\psi}_i\right)}{\partial \alpha }=\left(f\left(\left(\widehat{\alpha}+\varDelta \widehat{\alpha}\right),\widehat{n},{\psi}_i\right)-f\left(\left(\widehat{\alpha}-\varDelta \widehat{\alpha}\right),\widehat{n},{\psi}_i\right)\right)/\left(2\varDelta \widehat{\alpha}\right) $$

(11)

$$ \frac{\partial f\left(\widehat{\beta},{\psi}_i\right)}{\partial n}=\left(f\left(\widehat{\alpha},\left(\widehat{n}+\varDelta \widehat{n}\right),{\psi}_i\right)-f\left(\widehat{\alpha},\left(\widehat{n}-\varDelta \widehat{n}\right),{\psi}_i\right)\right)/\left(2\varDelta \widehat{n}\right) $$

(12)

where Δ = 0.015, $ \widehat{\alpha} $ and $ \widehat{n} $ are optimized value of α and n, respectively.

The estimated asymptotic covariance matrix (V) of the estimated parameters can be obtained by (Fox and Weisberg 2010):

$$ V=\left[\begin{array}{cc}\hfill {\delta}_{\alpha \alpha}^2\hfill & \hfill {\delta}_{\alpha n}^2\hfill \\ {}\hfill {\delta}_{n\alpha}^2\hfill & \hfill {\delta}_{nn}^2\hfill \end{array}\right]={\sigma}^2{\left({\boldsymbol{F}}^{\boldsymbol{\hbox{'}}}\boldsymbol{F}\right)}^{-1} $$

(13)

where (F ^′ F)^− 1 is the inverse of F ^′ F, and F ^′ is a transpose of F.

The σ ² can be approximated by dividing the SSE by the degree of freedom, df, as in the form (Brown 2001):

$$ {\sigma}^2=\frac{SSE}{df} $$

(14)

where df is calculated as the number of observations in the sample minus the number of parameters. In this study, df equals 14 (i.e., 16 minus 2).

Therefore, $ {\delta}_{\alpha \alpha}^2 $, $ {\delta}_{nn}^2 $, $ {\delta}_{\alpha n}^2 $ ( or $ {\delta}_{n\alpha}^2 $) in Eq. (13) are the estimated variance of α, variance of n, and covariance of α and n, respectively. Specifically, δ _αα and δ _nn are the standard errors used to characterize the uncertainties of α and n, respectively. At 95% confidence, the intervals of α and n are $ \widehat{\alpha} $ ±1.96 δ _αα, $ \widehat{n} $ ±1.96 δ _nn, respectively. SigmaPlot 10.0 is used to estimate the parameters and associated standard errors.

Monte Carlo method to estimate parameter uncertainty

Monte Carlo method is an analytical technique for solving a problem by performing a large number of simulations and inferring a solution from the collective results of the simulations. It is a method to calculate the probability distribution of possible outcomes.

In this paper, Monte Carlo simulation is performed to obtain residues of dependent variable θ. The residues follow a specified distribution with a mean of zero and standard deviation of $ \sqrt{SSE/df} $. The simulated residues are added to the predicted θ ($ \widehat{\theta} $) to reconstruct new observations for dependent variable θ. The expression for obtaining new observations for dependent variable θ in Excel is:

$$ \theta =\widehat{\theta}+\mathrm{NORM}.\mathrm{I}\mathrm{N}\mathrm{V}\left(\mathrm{RAND}\left(\right),0,\mathrm{SQRT}\left(\frac{SSE}{df}\right)\right) $$

(15)

where function NORM.INV gives a value which follow a normal distribution with a mean of zero and standard deviation of $ \sqrt{SSE/df} $ at a probability of RAND(). Therefore, normal distribution on the θ is assumed for Monte Carlo method. Excel function RAND produces a random value that is greater than or equal to 0 and less than 1. SQRT is a function to obtain the square root of a variable.

Monte Carlo simulations are performed 2000 times. Nonlinear regression is made on the simulated θ values versus |ψ| to obtain 2000 values for parameters α and n. The fitted values with different numbers (from 100 to 2000 with intervals of 100) of simulation is analyzed separately to determine the influences of number of simulation on uncertainty estimates. For each dataset, the probability distribution of α and n will be determined by the Shapiro-Wilk test using SPSS 16.0, and the 95% confidence intervals of α and n will be calculated to represent their uncertainties. For simplification, only 200 simulations are shown as an example. Readers can run different numbers of simulation by analogy.

Bootstrap method to estimate parameter uncertainty

Bootstrap method is an alternative method first introduced by Efron (1979) for determining uncertainty in any statistic caused by sampling error. The main idea of this method is to resample with replacement from the sample data at hand and create a large number of “phantom samples” known as bootstrap samples (Singh and Xie 2013). Bootstrap method is a nonparametric method which requires no assumptions about the data distribution.

Residues of θ are calculated by subtracting the $ \widehat{\theta} $ from the original θ measurements. Bootstrap method is used to resample the residues with replacement for each θ from the calculated residues. The re-sampled residues are added to the $ \widehat{\theta} $ to reconstruct new observations for dependent variable θ. The expression for obtaining new observations for dependent variable θ using bootstrap method in Excel is:

$$ \theta =\widehat{\theta}+\mathrm{INDEX}\Big(\mathrm{Range}\ \mathrm{of}\ \mathrm{residual},\mathrm{I}\mathrm{N}\mathrm{T}\left(\mathrm{RAND}\left(\right)*\mathrm{Row}\ \mathrm{number}\right) $$

(16)

where function INDEX is used to randomly return a calculated residual from a certain array. Range of residual refers to the calculated residues. INT is a function to round a given number, which is randomly produced by RAND() multiplied by row number.

The non-parametric bootstrap method is a special case of Monte Carlo method used for obtaining the distribution of residues of θ which can be representative of the population. The idea behind the bootstrap method is that the calculated residues can be an estimate of the population, so the distribution of the residues can be obtained by drawing many samples with replacement from the calculated residues. For the Monte Carlo method, however, it creates the distribution of residues of θ with a theoretical (i.e., normal) distribution. From this aspect, the bootstrap method is more empirically based and the Monte Carlo method is more theoretically based.

Similar to the Monte Carlo method, bootstrap simulations are performed 2000 times. Distribution type and 95% confidence intervals of α and n will also be determined for fitted datasets with different numbers (from 100 to 2000 with intervals of 100) of simulation. For simplification, only 200 simulations are shown as an example.

Declarations

Acknowledgements

The project was funded by the Natural Sciences and Engineering Research Council (NSERC) of Canada.

Authors’ Affiliations

(1)

Department of Soil Science, University of Saskatchewan, Saskatoon, Canada

(2)

Department of Soil and Physical Science, Lincoln University, Christchurch, New Zealand

References

Berger RL (2007) Nonstandard operator precedence in Excel. Comput Stat Data An 51:2788–2791View ArticleGoogle Scholar
Brown AM (2001) A step-by-step guide to non-linear regression analysis of experimental data using a Microsoft Excel spreadsheet. Comp Meth Prog Bio 65:191–200View ArticleGoogle Scholar
Conedera M, Torriani D, Neff C, Ricotta C, Bajocco S, Pezzatti GB (2011) Using Monte Carlo simulations to estimate relative fire ignition danger in a low-to-medium fire-prone region. Forest Ecol Manag 26:2179–2187View ArticleGoogle Scholar
Cwiertny DM, Roberts AL (2005) On the nonlinear relationship between k(obs) and reductant mass loading in iron batch systems. Environ Sci Technol 39:8948–8957View ArticleGoogle Scholar
Delboy H (1994) A non-linear fitting program in pharmacokinetics with Microsoft® Excel spreadsheet. Int J Biomed Comput 37:1–14View ArticleGoogle Scholar
Efron B (1979) Bootstrap method: another look at the Jackknife. Ann Stat 7:1–26View ArticleGoogle Scholar
Efron B, Tibshirani R (1993) An introduction to the Bootstrap. Champman & Hall, London, UKView ArticleGoogle Scholar
Fox J, Weisberg S (2010) Nonlinear regression and nonlinear least squares in R: An appendix to an R companion to applied regression, second edition. http://socserv.socsci.mcmaster.ca/jfox/Books/Companion/appendix/Appendix-Nonlinear-Regression.pdf.
Fredlund DG, Xing AQ, Huang SY (1994) Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can Geotech J 31:533–546View ArticleGoogle Scholar
Han XW, Shao MA, Hortaon R (2010) Estimating van Genuchten model parameters of undisturbed soils using an integral method. Pedosphere 20:55–62View ArticleGoogle Scholar
Harris DC (1998) Nonlinear least-squares curve fitting with Microsoft Excel Solver. J Chem Educ 75:119–121View ArticleGoogle Scholar
Luo B, Maqsood I, Yin YY, Huang GH, Cohen SJ (2003) Adaption to climate change through water trading under uncertainty - An inexact two-stage nonlinear programming approach. J Environ Inform 2:58–68View ArticleGoogle Scholar
Singh K, Xie M (2013) Bootstrap: A statistical method. From Rutgers University. http://www.stat.rutgers.edu/home/mxie/rcpapers/bootstrap.pdf.
Smith LH, McCarty PL, Kitanidis PK (1998) Spreadsheet method for evaluation of biochemical reaction rate coefficients and their uncertainties by weighted nonlinear least-squares analysis of the integrated Monod equation. Appl Environ Microbiol 64:2044–2050Google Scholar
Tong L, Chang C, Jin S, Saminathan R (2012) Quantifying uncertainty of emission estimates in National Greenhouse Gas Inventories using bootstrap confidence intervals. Atmos Environ 56:80–87View ArticleGoogle Scholar
van Genuchten MT (1980) A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci Soc Am J 44:892–898View ArticleGoogle Scholar
Wang QJ, Horton R, Shao MA (2002) Horizontal infiltration method for determining Brooks-Corey model parameters. Soil Sci Soc Am J 66:1733–1739View ArticleGoogle Scholar
Wraith JM, Or D (1998) Nonlinear parameter estimation using spreadsheet software. J Nat Resour Life Sci Educ 27:13–19Google Scholar

Copyright

This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.